During recent projects I came across two concepts teacher forcing and scheduled sampling. Teacher forcing is a technique to train recurrent neural networks (rnns). Where as scheduled sampling is more a general probability sampling method, which could be used in more scenarios.
Teacher forcing
In complex challenges like for example sound event detection (SED) there might be multiple training objectives. SED comes with two objectives:
- predict classes
- predict event boundaries
To meet both objectives with one network one could train a CRNN (convolutional recurrent network). The problem when training the RNN on top of the CNN is a very general problem: Since the recurrency works by passing the previous states, predicting the early state falsly propagates the error through the time steps and slows down training.
Teacher forcing leak
targetsduring training at randomly chosen time steps with some probability to hint the model towards the correct learning path.
This seams like cheating, and exploits the training prcoess to potential overfitting, so one has to choose the probability wisely or the model will dramatically overfit.
Example model
As a basis for this process I rely on the illustrations and strategy chosen by K. Drossos et.al.: Language modelling for sound event detection with teacher forcing and scheduled sampling. Their publication uses a CRNN (a RNN head with CNN blocks as a basis), to train spectogram sequences of the DCase Tasks of 2016 and 2017.
First we need some features. Here I’d like to recommend torchlibrosa.
Be aware both Spectrogram and LogmelFilterBank are coming from torchlibrosa.
We do the same as Drossos et.al.:
class FeatureExtractor(nn.Module):
def __init__(
self,
window_len: int,
hop_len: int,
sample_rate: int,
n_mels: int,
n_fft: int,
is_log: bool,
):
super(FeatureExtractor, self).__init__()
self.module = nn.Sequential(
Spectrogram(n_fft, hop_len, window_len),
LogmelFilterBank(sample_rate, n_fft, n_mels, is_log=is_log),
)
def forward(self, inputs: Tensor) -> Tensor:
return self.module(inputs)
if __name__ == "__main__":
sample_wav = download_asset(
"tutorial-assets/Lab41-SRI-VOiCES-src-sp0307-ch127535-sg0042.wav"
)
waveform, sr = torchaudio.load(sample_wav)
print(waveform.size(), sr)
# torch.Size([1, 54400]) 16000
feature_module = FeatureExtractor(1024, 512, sr, 40, 2048, False)
print(feature_module(waveform).size())
# torch.Size([1, 1, 107, 40])
y = torch.randint(low=0, high=2, size=(107, 6)).unsqueeze(0)
print(y.size())
# torch.Size([1, 107, 6])
Note we generated some random class targets with a shape of (1, 107, 6), where 1 is the
batch_size, 107 is the number of timesteps and 6 our number of classes. Up next we need a
model with an RNN head, we’ll also use the proposed one of Drossos et.al.:
def init_dropout(module: Module, p: float):
for mod in module.modules():
if isinstance(mod, Dropout):
mod.p = p
class ConvolutionBlock(Module):
def __init__(
self,
in_channels: int,
out_channels: int,
maxpool_kernel_size: Union[int, Tuple[int, int]],
maxpool_stride: Union[int, Tuple[int, int]],
):
super(ConvolutionBlock, self).__init__()
self.module = Sequential(
Conv2d(in_channels, out_channels, kernel_size=5, stride=1, padding=2),
BatchNorm2d(out_channels),
ReLU(),
MaxPool2d(kernel_size=maxpool_kernel_size, stride=maxpool_stride),
)
def forward(self, inputs: Tensor) -> Tensor:
return self.module(inputs)
class CRNN(Module):
def __init__(
self,
conv_dims: int,
rnn_hidden_dims: int,
num_classes: int,
dropout: float,
window_len: int = 1024,
hop_len: int = 512,
sample_rate: int = 16000,
n_mels: int = 40,
n_fft: int = 2048,
is_log: bool = False,
):
super(CRNN, self).__init__()
self.feature_module = FeatureExtractor(
window_len=window_len,
hop_len=hop_len,
sample_rate=sample_rate,
n_mels=n_mels,
n_fft=n_fft,
is_log=is_log,
)
self.convolutions = Sequential(
ConvolutionBlock(1, conv_dims, (1, 5), (1, 5)),
ConvolutionBlock(conv_dims, conv_dims, (1, 4), (1, 4)),
ConvolutionBlock(conv_dims, conv_dims, (1, 2), (1, 2)),
)
self.rnn = GRUCell(conv_dims + num_classes, rnn_hidden_dims, bias=True)
self.fnn = Linear(rnn_hidden_dims, num_classes, bias=True)
self.num_classes = num_classes
init_dropout(self, dropout)
They use three convolution blocks that differ in the kernel_size and stride of the
max pooling layer. On top of that they use a GRUCell as the recurrency network and a
single fully connected layer accepting the output of the RNN and outputting the number
of classes. The last layer is also known as feed-forward neural network (FNN/FFN).
Their design focuses on the design of the gradient recurrent unit (GRUCell), which
has a slightly different input (conv_dims + num_classes). Like this they can first input
the to the feature_module and the convolutions, to then concat this output with the
RNNs output and randomly force the forward-step to concat the convolutions with
the correct targets of a timestep t. If they randomly select not to leak the targets
of t-th timestep they select the output of the former classification step as input for
the RNN. The process looks like this:
@property
def teacher_forcing_prob(self) -> float:
return 0.7 # This will change when using scheduled sampling!
def get_forced_targets(self, batch_size: int, is_inference: bool) -> Tensor:
if is_inference:
return torch.zeros(batch_size)
return torch.rand(batch_size).lt_(self.teacher_forcing_prob)
def forward(self, inputs: Tensor, targets: Optional[Tensor] = None) -> Tensor:
features = self.feature_module(inputs)
B, _, T, M = features.size()
C = self.num_classes
features = self.convolutions(features).permute(0, 2, 1, 3)
features = features.squeeze(-1)
teacher_force = torch.zeros(B, C)
h = torch.zeros(B, self.rnn.hidden_size)
outputs = torch.zeros(B, T, self.num_classes)
for t in range(T):
rnn_features = torch.cat([features[:, t, :], teacher_force], dim=-1)
h = self.rnn(rnn_features, h)
out = self.fnn(h)
rnn_inputs = out.sigmoid().gt(.5).float()
force_targets = self.get_forced_targets(B, (targets is None))
for batch_idx, force in enumerate(force_targets):
teacher_force[batch_idx, :] = (
targets[batch_idx, t, :] if force else rnn_inputs[batch_idx, :]
)
outputs[:, t, :] = out
return outputs
The important in the above forward-step is the decision wether or not to use the correct
targets, which is performed at every timestep t:
force_targets = self.get_forced_targets(B, (targets is None))
for batch_idx, force in enumerate(force_targets):
teacher_force[batch_idx, :] = (
targets[batch_idx, t, :] if force else rnn_inputs[batch_idx, :]
)
Not that we keep all the original out variables in outputs, so the loss is later
correctly calculated (outputs[:, t, :] = out).
Scheduled sampling
Scheduled sampling (in this case) is a method to sample probabilities for the controlled use of teacher forcing. This concept aims to guide the training during the crucial first iterations.
Teacher forcing will only thrive in sequence prediction if combined with a good sampling strategy. Scheduled sampling was proposed by S. Bengio et.al. in Scheduled Sampling for Sequence Prediction with Recurrent Neural Networks. They propose their strategy for different sequence prediction applications, like Image Captioning, Constituency Parsing and Speech Recognition. Their strategy consists of a decreasing function which can have different properties e.g. linear, sigmoid or exponential.
The strategy by Drossos et.al. is linked to the number of batches, to control the decrease of teacher-forcing probability with iterations the model was trained on. They discribe it as:
$$ p_{tf} = min(p_{max}, 1 - min(1 − p_{min}, \frac{2}{1 + e^{\beta}} - 1)),\ where\ \beta = -\gamma \frac{i}{N_{b}} $$
This is an expoential decrease, where \( e^{ \beta } \) is the decreasing factor, because i is rising with each iteration a new probability is sampled and N is the number of batches in a single epoch and \( \gamma \) controlls the slope.
This way the training process can sample a new probability everytime a new batch arrives or during the sequential prediction for every timestep. To visualize the samples we can use the slope that will be influenced by \( \gamma \) here’s a small illustration of how it’s build:
class ScheduledSampler(nn.Module):
def __init__(
self,
num_batches: int,
gamma: float,
p_min: float = 0.05,
p_max: float = 0.95,
):
super(ScheduledSampler, self).__init__()
self.N = num_batches
self.gamma = gamma
self.p_min = p_min
self.p_max = p_max
self.iteration = 0
@property
def exp_beta(self) -> float:
return Tensor([-self.gamma * (self.iteration / self.N)]).exp().item()
def forward(self, batch_size: int) -> Tuple[Tensor, float]:
p = min(self.p_max, 1 - min(1 - self.p_min, (2 / (1 + self.exp_beta)) - 1))
return torch.rand(batch_size).lt_(p), p
def update_iteration(self) -> None:
self.iteration += 1
The following example assumes a few parameters, initilizes a sampler for each configuration
and runs N * T weight updates to generate some probabilities. Just for clarification
T is the parameter for the time steps in the inputs/target data shape, which is
also the number of times the RNN predicts per sample.
if __name__ == "__main__":
N = 50
B = 16
T = 107
sampler_config = [
{"gamma": 0.01, "p_min": 0.05, "p_max": 0.95},
{"gamma": 0.02, "p_min": 0.05, "p_max": 0.9},
{"gamma": 0.08, "p_min": 0.025, "p_max": 0.8},
{"gamma": 0.10, "p_min": 0.01, "p_max": 0.7},
]
samplers = [ScheduledSampler(N, **conf) for conf in sampler_config]
sampled_probs = [[], [], [], []]
for _ in range(N * T):
for idx, sampler in enumerate(samplers):
sampled_probs[idx].append(sampler(B)[1])
sampler.update_iteration()
for idx in range(len(samplers)):
label = ", ".join([f"{k}:{v}" for k, v in sampler_config[idx].items()])
plt.plot(np.arange(len(sampled_probs[idx])), sampled_probs[idx], label=label)
plt.legend()
plt.xlabel("Iteration")
plt.ylabel("Probabiliy")
plt.tight_layout()
plt.savefig("scheduled_sampler_plots.png")
plt.show()
The result shows the higher gamma the faster p_min is hit. Also it shows well how the
first iterations are capped by the p_max parameter. The number of batches N (in the
training dataset) together with the models/samplers current iteration together with
gamma controlls the decrease, such that the model does not overfit fast, but the rnn
training is still guided efficiently.
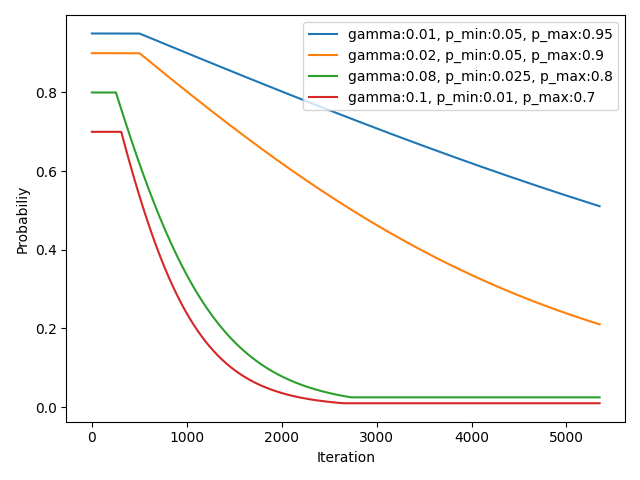
Sampling strategy by Bengio et.al. with different configurations. Slope of sampled probabilities is controlled by the gamma.
Both together
If we plug this sampler into the model we can generate a new probability each time,
either when a new batch arrives or when the rnn predicts a new time step. The latter
scenario is the case for teacher-forcing. Just adapt the __init__ of CRNN to
recieve tf_prob_sampler: ScheduledSampler and add it to the module, so the scheduler
can be used with self.tf_prob_sampler. The rest is done in get_forced_targets.
class CRNN(Module):
def __init__(
self,
conv_dims: int,
rnn_hidden_dims: int,
num_classes: int,
dropout: float,
tf_prob_sampler: ScheduledSampler, # Provide the module
window_len: int = 1024,
hop_len: int = 512,
sample_rate: int = 16000,
n_mels: int = 40,
n_fft: int = 2048,
is_log: bool = False,
):
self.tf_prob_sampler = tf_prob_sampler
# ...
def get_forced_targets(
self, batch_size: int, is_inference: bool
) -> Tuple[Tensor, float]:
if is_inference:
return torch.zeros(batch_size), 0.0
force_targets, p = self.tf_prob_sampler(batch_size)
self.tf_prob_sampler.update_iteration()
return force_targets, p
In the following I generated sample teacher-forcing draws to simulate what it would feel
like when training a model. We return both the targets_forced plus sampled_probs from
the forward call and plot while training epochs rise and so do the samplers
iteration values.
Here is a simulation with
- 50 batches
- batch_size 16
- each sample with 107 time steps
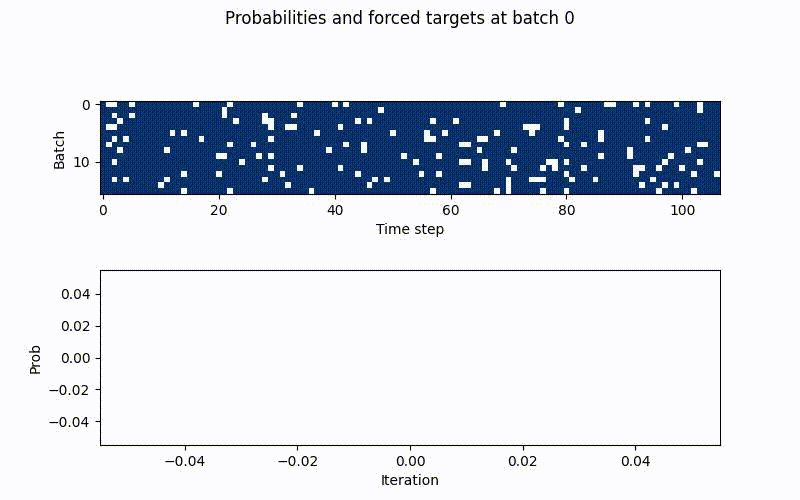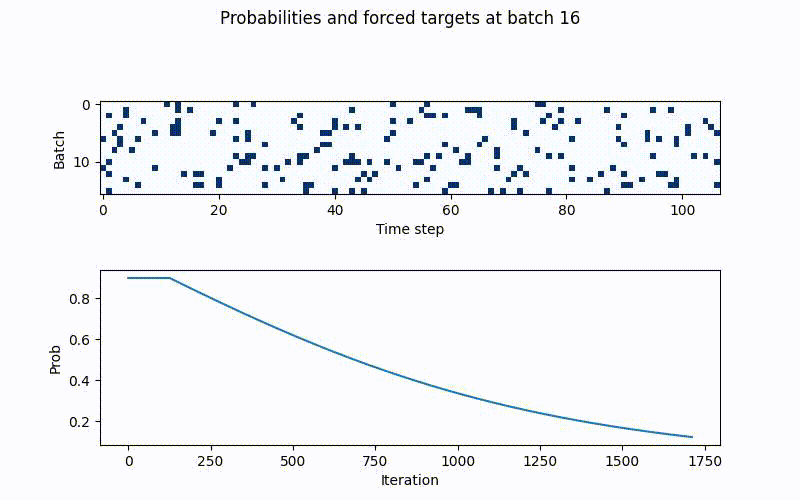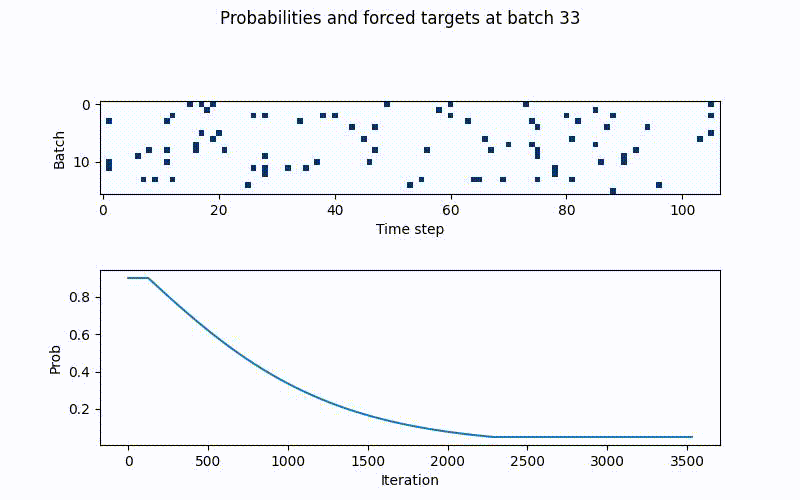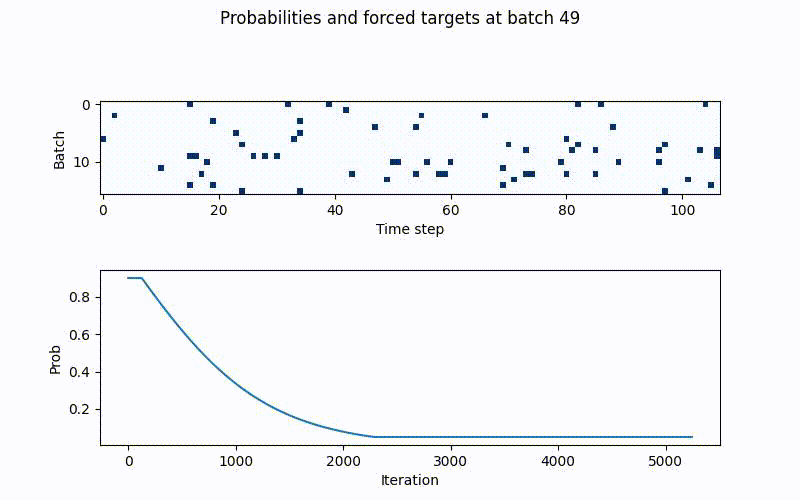
The above schedule with gamma=0.08 (bottom), together with the forced samples per batch and timestamp (top). Blue tiles are teacher forced targets and replaced in the batch and timestamp for the RNNs prediction in t+1. White tiles are rnn predictions.
In the beginning there is clear a lot of blue tiles (true targets) are passed to the rnn
inputs, meaning the rnns original prediction is replaced with true targets in these
time steps, whereas the white ones are original prediction. As the iterations rise, these
drop drastically in frequency until p_min is hit. Like this scheduled sampling as a
guiding effect to the rnns training, without overfitting instantly.
PS: If you want to replicate the experiment: All sources are available at github.com/arrrrrmin/arrrrrmin.netlify.com Enjoy 🎉